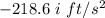Answer:
a) the angular acceleration of the bar AB is
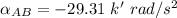
b) the acceleration
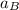 of point B =
of point B =
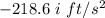
Step-by-step explanation:
The sketched diagram below shows an illustration of what the question comprises of:
Now, from the diagram ; we can deduce the following relations;
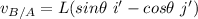
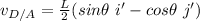
Taking point H as the instantaneous center of rotation of line HD. The distance between H and D is represented as:
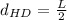
The angular velocity of the bar AB from the diagram can be determined by using the relation:
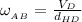
where:
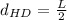
and
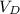 = velocity of point D = 18.5 ft/s
= velocity of point D = 18.5 ft/s
L = length of the bar = 8 ft
Then;
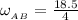
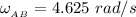
Using vector approach to acceleration analysis;
Acceleration about point B can be expressed as;
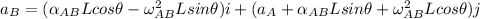 ---equation(1)
---equation(1)
The y - component of
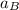 ⇒
⇒
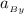 =
=
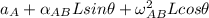
where;
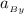 = 0
= 0
Then
0 =
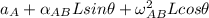
Making
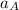 the subject of the formula; we have:
the subject of the formula; we have:
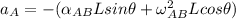 ------- equation (2)
------- equation (2)
Acceleration about point D is expressed as follows:
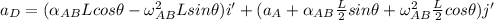
The y - component of
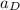 ⇒
⇒
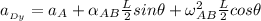
Replacing - 23 ft/s² for
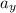 ; we have:
; we have:
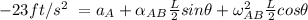
Also; replacing equation (2) for
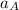 in the above expression; we have
in the above expression; we have
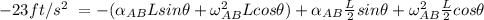
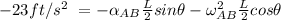
Making
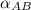 the subject of the formula ; we have:
the subject of the formula ; we have:
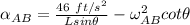
Replacing 8 ft for L; 27° for θ; 4.625 rad/s for
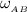
Then;
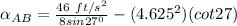
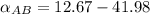
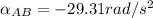
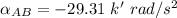
Thus, the angular acceleration of the bar AB is
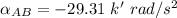
b)
To calculate the acceleration of point B using equation (1); we have:
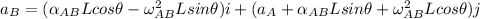
Replacing
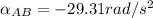
L = 8 ft
θ = 27°
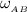 = 4.625 rad/s
= 4.625 rad/s
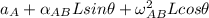 = y = 0
= y = 0
Then;
![a_B = [-29.31(8)cos 27^0- (4.625^2)(8sin27^0)] i +0j](https://img.qammunity.org/2021/formulas/physics/college/3rjnvwa3zcnffdu7ttjhdyk5y18sb87p3f.png)
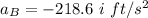
Thus, the acceleration
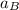 of point B =
of point B =