Question

A 1.01 kg mass is attached to a spring of force constant 10.1 N/cm and placed on a frictionless surface. By how much will the spring stretch if the mass moves along a circular path of radius 0.515 m at a rate of 1.84 revolutions per second

Answer 1

6.88 cm

Step-by-step explanation:

Given that:

mass m of the object = 1.0 kg

Force constant of the spring (k) = 10.1 N/cm = 10.1 × (100) N/m

= 1010 N/m

Radius of the circular path R = 0.515 m

Since 1 revolution = 2 π radian

angular speed of the object ω = 1.84 rev/s = 1.84 × ( 2 π) rad/s

= 11.56 rad/s

Amount of the spring that stretches = X???

However, the amount of the force the spring exerts on the object due to the stretching is directly equal to the centripetal force required by the object for the circular motion:

SO;

`K(X) = m \omega^2 R\\1010*(X) = 1.01 *(11.56)^2 *0.515 \\(X) = (1.01*(11.56)^2*0.515)/(1010) \\(X) = 0.0688`

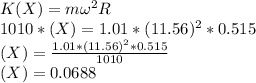
X = 0.0688 m

Hence, the amount of the spring stretches = 6.88 cm