Answer:
(a) 422.2 x 10⁻⁷m
(b) 4.6 x 10⁵ Hz
Step-by-step explanation:
The magnetic force acting perpendicular to the velocity of the electron will cause a circular motion so that the centripetal force,
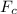 , of the electron is equal to the Lorentz's force,
, of the electron is equal to the Lorentz's force,
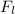 . i.e
. i.e
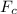 =
=
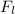 ---------------(i)
---------------(i)
Where;
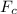 =
=
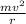
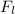 = qvB
= qvB
Equation (i) then becomes;
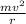 = qvB ------------------(ii)
= qvB ------------------(ii)
Where;
m = mass of the electron
v = linear velocity of the electron
r = radius of the electron's path
q = charge of the electron
B = magnetic field.
Make r subject of the formula in equation (ii)
r =

r =
 -----------(iii)
-----------(iii)
From the question;
v = 121m/s
B = 1.63 x 10⁻⁵ T
q = 1.6 x 10⁻¹⁹ C (known constant)
m = 9.1 x 10⁻³¹kg
Substitute these values into equation (iii) as follows;
r =
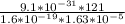
r = 422.2 x 10⁻⁷m
Therefore, the radius of the electron's path is 422.2 x 10⁻⁷m
(ii) The frequency, f, of the motion which is also called the cyclotron frequency - the number of cycles the electron completes around the path every second - is given by;
f =

Substitute the values of v and r into the equation as follows;
f =
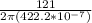
Take
 = 3.142
= 3.142
f =
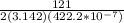
f = 4.6 x 10⁵ Hz
Therefore, the frequency of the motion is 4.6 x 10⁵ Hz