Question

The time between customers is exponentially distributed with a mean of 0.5 minutes. Given that 60 minutes have elapsed since the last customer, find the probability that we must wait an additional 5 mins for the arrival of the next customer

Answer 1

The probability that we must wait 5 more minutes is 0.0000454

Explanation:

Let X be the amount of minutes that passed between the two customers. X has emponential distribution with parameter
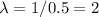`\lambda = 1/0.5 = 2` and its density is

`f_X(x) = 2 \, e^(-2 \, x)`

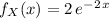
We want to compute is P(X> 65 | X > 60), which is equal to P(X>65)/P(X>60) (Because the conditional event is contained in the other event). Lets do some computations

`P(X>60) = \int\limits_(60)^(+\,\infty) {2e^(-2 \, x) } \, dx = - e^(-2x) \, |^(+\infty)_(\, 60) =e^(-120)`

`P(X>65) = \int\limits_(65)^(+\,\infty) {2e^(-2 \, x) } \, dx = - e^(-2x) \, |^(+\infty)_(\, 65) = e^(-130)`

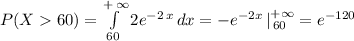
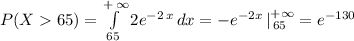
As a consequence

`P(X > 65 | X > 60) = (P(X > 65))/(P(X>60)) = (e^(-130))/(e^(-120)) = e^(-10) = 0.0000454`

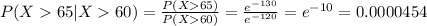
Note that this is the same result than just calculate P(X > 5), and 5 is, by the way, the difference between 60 and 65. This is commonly referred as the memoryless property: The past doesnt have influence in the future.

We conclude that the probability that we must wait 5 more minutes is 0.0000454.