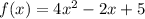Question

Find the particular solution of the differential equation that satisfies the initial conditions. f apostrophe apostrophe open parentheses x close parentheses equals 8 comma space space space space f apostrophe (1 )equals 6 comma space space space space f (0 )equals 5

Answer 1

Therefore the required solution is

`f(x)=4x^2-2x+5`

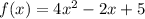
Explanation:

Rule of integration:

1. 
   `\int x^ndx=(x^(n+1))/(n+1)+C`
2. 
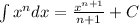
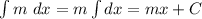   `\int m\ dx = m\int dx= mx+C` [ m is a constant]
3. 
   `\int mx^ndx=m\int x^n dx=m.(x^(n+1))/(n+1)`

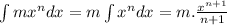
Given that,

f''(x) = 8 and initial conditions are f'(1)=6 and f(0)=5

∴f''(x) = 8

Integrating both sides

`\int f''(x) dx=\int 8 dx`

`\Rightarrow f'(x)= 8x+C_1` [
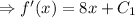`C_1` is constant of integration]

Initial condition f'(1) =6

`\therefore 6= 8.1+C_1`

`\Rightarrow C_1=6-8`

`\Rightarrow C_1=-2`

`\therefore f'(x)=8x-2`

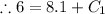
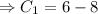
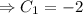
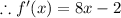
Again integrating both sides

`\int f'(x) dx=\int8x dx- \int2dx`

`\Rightarrow f(x)=8(x^2)/(2)-2x+C_2` [
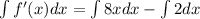
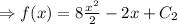`C_2` is constant of integration]

`\Rightarrow f(x)=4x^2-2x+C_2`

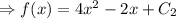
Initial condition f(0)=5

`5=4.0^2-2.0+C_2`

`\Rightarrow C_2=5`

`\therefore f(x)=4x^2-2x+5`

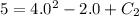
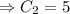
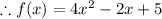
Therefore the required solution is

`f(x)=4x^2-2x+5`