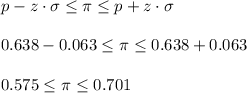Question

The U.S. Department of Education reported that in 2007, 67% of students enrolled in college or a trade school within 12 months of graduating from high school, in 2013, a random sample of 160 individuals who graduated from high school 12 months prior was selected. From this sample, 102 students were found to be enrolled in college or a trade school. A.) construct a 90% confidence interval to estimate the actual proportion of students enrolled in college or a trade school within 12 months of graduating from high school in 2013. B.) What is the margin of error for this sample

Answer 1

a) The 90% confidence interval is
`0.575\leq \pi\leq 0.701`

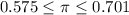
b) The margin of error is 0.063.

Explanation:

We have to construct a 90% confidence interval for the proportion of students enrolled in college or a trade school within 12 months of graduating from high school in 2013.

We have a sample of 160 students, and a proportion of:

`p=X/N=102/160=0.6375`

The standard deviation is:

`\sigma=\sqrt{(p(1-p))/(N)}=\sqrt{(0.6375*0.3625)/(160)}=0.038`

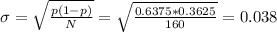
As the sample size is big enough, we use the z-value as statistic. For a 90% CI, the z-value is z=1.645.

Then, the margin of error is:

`E=z\cdot\sigma=1.645\cdot 0.038=0.063`

Then, the 90% confidence interval is:

`p-z\cdot \sigma\leq \pi\leq p+z\cdot\sigma\\\\0.638-0.063\leq \pi\leq 0.638+0.063\\\\0.575\leq \pi\leq 0.701`