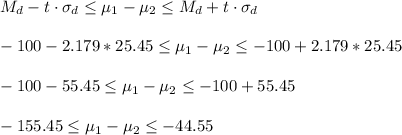Question

Let us suppose we have data on the absorbency of paper towels that were produced by two different manufacturing processes. From process 1, the sample size was 10 and had a mean and standard deviation of 200 and 15, respectively. From process 2, the sample size was 4 with a mean and standard deviation of 300 and 50, respectively.

Answer 1

The 95% CI for the difference of means is:

`-155.45 \leq \mu_1-\mu_2 \leq -44.55`

Explanation:

The question is incomplete:

"Find a 95% confidence interval on the difference of the towels mean absorbency produced by the two processes. Assumed that the standard deviations are estimated from the data. Round to two decimals places."

Process 1:

- Sample size: 10

- Mean: 200

- S.D.: 15

Process 2:

- Sample size: 4

- Mean: 300

- S.D.: 50

The difference of the sample means is:

`M_d=M_1-M_2=200-300=-100`

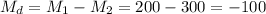
The standard deviation can be estimated as:

`\sigma_d=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}\\\\\sigma_d=\sqrt{(15^2)/(10)+(50^2)/(4)} =√(22.5+625)=√(647.5)=25.45`

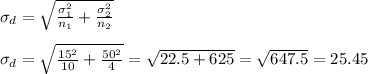
The degrees of freedom are:

`df=n_1+n_2-2=10+4-2=12`

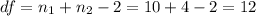
The t-value for a 95% confidence interval and 12 degrees of freedom is t=±2.179.

Then, the confidence interval can be written as:

`M_d-t\cdot \sigma_d\leq \mu_1-\mu_2 \leq M_d+t\cdot \sigma_d\\\\-100-2.179*25.45\leq \mu_1-\mu_2 \leq -100+2.179*25.45\\\\-100-55.45 \leq \mu_1-\mu_2 \leq -100+55.45\\\\ -155.45 \leq \mu_1-\mu_2 \leq -44.55`