Question

Suppose that the functions S and tea are defined for all real numbers X as follows S(x)=x-5 t(x)=3xsqaured write the expression for (t-s)(x) and (t+s)(x) and evaluate (t•s)(3)

Answer 1

The correct answer is (t-s)(x) = 3
`x^(2)` - x + 5; (t+s)(x) = 3
`x^(2)` + x - 5; (t·s)(3) = -54.

Explanation:

Function s is defined as the following: s(x) = x - 5.

Function t is defined as the following: t(x) = 3
`x^(2)` .

Assuming that the two functions are defined on the same domain,

(t-s)(x) = t(x) - s(x) = 3
`x^(2)` - x + 5.

(t+s)(x) = t(x) + s(x) = 3
`x^(2)` + x - 5.

(t·s)(x) = t(x) × s(x) = 3
`x^(2)` × (x -5)

(t·s)(3) = t(3) × s(3) = 3 ×
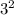`3^(2)` × (3 -5) = - 54

The required functions are given above and the value of the multiplication function at x = 3 is -54.