Question

Television viewing reached a new high when the global information and measurement company reported a mean daily viewing time of hours per household. Use a normal probability distribution with a standard deviation of hours to answer the following questions about daily television viewing per household. a. What is the probability that a household views television between 3 and 9 hours a day (to 4 decimals)? b. How many hours of television viewing must a household have in order to be in the 2%top of all television viewing households (to 2 decimals)? hours c. What is the probability that a household views television more than hours a day (to 4 decimals)?

Answer 1

(a) The probability that a household views television between 3 and 9 hours a day is 0.5864.

(b) The viewing hours in the top 2% is 13.49 hours.

(c) The probability that a household views television more than 5 hours a day is 0.9099.

Explanation:

Let X = daily viewing time of of television hours per household.

The mean daily viewing time is, μ = 8.35 hours.

The standard deviation of daily viewing time is, σ = 2.5 hours.

The random variable X is Normally distributed.

To compute the probability of a Normal random variable, first we need to compute the raw scores (X) to z-scores (Z).

`z=(x-\mu)/(\sigma)`

(a)

Compute the probability that a household views television between 3 and 9 hours a day as follows:

`P(3<X<9)=P((3-8.35)/(2.5)<(X-\mu)/(\sigma)<(9-8.35)/(2.5))`

`=P(-2.14<Z<0.26)\\=P(Z<0.26)-P(Z<-2.14)\\=0.60257-0.01618\\=0.58639\\\approx0.5864`

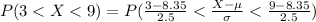
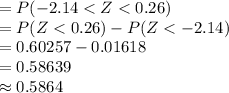
Thus, the probability that a household views television between 3 and 9 hours a day is 0.5864.

(b)

Let the viewing hours in the top 2% be denoted by x.

Then,

P (X > x) = 0.02

⇒ P (X < x) = 1 - 0.02

P (X < x) = 0.98

⇒ P (Z < z) = 0.98

The value of z for the above probability is:

z = 2.054

*Use a z-table for the value.

Compute the value of x as follows:

`z=(x-\mu)/(\sigma)\\2.054=(x-8.35)/(2.5)\\x=8.35+(2.054* 2.5)\\x=13.485\\x\approx13.49`

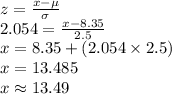
Thus, the viewing hours in the top 2% is 13.49 hours.

(c)

Compute the probability that a household views television more than 5 hours a day as follows:

`P(X>5)=P((X-\mu)/(\sigma)>(5-8.35)/(2.5))`

`=P(Z>-1.34)\\=P(Z<1.34)\\=0.90988\\\approx0.9099`

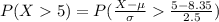
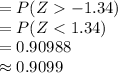
Thus, the probability that a household views television more than 5 hours a day is 0.9099.