Answer:
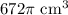 .
.
Explanation:
We have been given that a sphere has a radius of 8 centimeters. A second sphere has a radius of 2 centimeters. We are asked to find the difference of the volumes of the spheres.
We will use volume formula of sphere to solve our given problem.
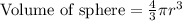 , where r is radius of sphere.
, where r is radius of sphere.
The difference of volumes would be volume of larger sphere minus volume of smaller sphere.


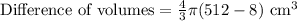
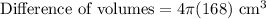
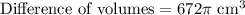
Therefore, the difference between volumes of the spheres is
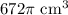 .
.