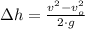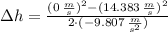Answer:

Step-by-step explanation:
The velocity of the ball just before the collision with one end of the bar is:
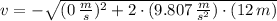
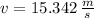
As the bar is pivoted at its center and collision is entirely inelastic, final velocity is determined by the Principle of Angular Momentum Conservation:
![(5\,kg)\cdot (-15.342\,(m)/(s) ) = \left\{-\left[(1)/(12)\cdot (8\,kg)\cdot (4\,m)^(2)\cdot ((1)/(2\,m) )+(5\,kg)\right] + (5\,kg)\right\}\cdot v](https://img.qammunity.org/2021/formulas/physics/high-school/var7pnph37ia9gba0qybkyxv21cs5om8el.png)
The final velocity of the another ball is:
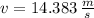
The maximum height of the other ball is: