Answer:
Within (1.9 , 3.7) intervals we would expect to find approximately 81.5% of all GPA's for students at this college.
Explanation:
We are given that the distribution of grade point averages for a certain college is approximately Normal with a mean of 2.5 and a standard deviation of 0.6.
Let X = distribution of grade point averages for a certain college
SO, X ~ Normal(
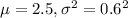 )
)
The z-score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 2.5
= population mean = 2.5
 = standard deviation = 0.6
= standard deviation = 0.6
Now, to find that within which interval we expect to find approximately 81.5% of all GPA's for students at this college, we will find respective probabilities for given intervals.
(a) P(0.7 < X < 3.1) = P(X < 3.1) - P(X
 0.7)
0.7)
P(X < 3.1) = P(
 <
<
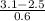 ) = P(Z < 1) = 0.84134
) = P(Z < 1) = 0.84134
P(X
 0.7) = P(
0.7) = P(


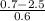 ) = P(Z
) = P(Z
 -3) = 1 - P(Z < 3)
-3) = 1 - P(Z < 3)
= 1 - 0.99865 = 0.00135
Therefore, P(0.7 < X < 3.1) = 0.84134 - 0.00135 = 0.8399
This means that in this interval we are able to find approximately 83.99% of all GPA's for students at this college.
(b) P(1.3 < X < 3.7) = P(X < 3.7) - P(X
 1.3)
1.3)
P(X < 3.7) = P(
 <
<
 ) = P(Z < 2) = 0.97725
) = P(Z < 2) = 0.97725
P(X
 1.3) = P(
1.3) = P(


 ) = P(Z
) = P(Z
 -2) = 1 - P(Z < 2)
-2) = 1 - P(Z < 2)
= 1 - 0.97725 = 0.02275
Therefore, P(1.3 < X < 3.7) = 0.97725 - 0.02275 = 0.9545
This means that in this interval we are able to find approximately 95.45% of all GPA's for students at this college.
(c) P(1.9 < X < 3.7) = P(X < 3.7) - P(X
 1.9)
1.9)
P(X < 3.7) = P(
 <
<
 ) = P(Z < 2) = 0.97725
) = P(Z < 2) = 0.97725
P(X
 1.9) = P(
1.9) = P(


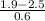 ) = P(Z
) = P(Z
 -1) = 1 - P(Z < 1)
-1) = 1 - P(Z < 1)
= 1 - 0.84134 = 0.15866
Therefore, P(1.9 < X < 3.7) = 0.97725 - 0.15866 = 0.8186
This means that in this interval we are able to find approximately 81.86% of all GPA's for students at this college.
(d) P(1.9 < X < 4.3) = P(X < 4.3) - P(X
 1.9)
1.9)
P(X < 4.3) = P(
 <
<
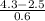 ) = P(Z < 3) = 0.99865
) = P(Z < 3) = 0.99865
P(X
 1.9) = P(
1.9) = P(


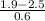 ) = P(Z
) = P(Z
 -1) = 1 - P(Z < 1)
-1) = 1 - P(Z < 1)
= 1 - 0.84134 = 0.15866
Therefore, P(1.9 < X < 4.3) = 0.99865 - 0.15866 = 0.8399
This means that in this interval we are able to find approximately 83.99% of all GPA's for students at this college.
(e) P(0.7 < X < 4.3) = P(X < 4.3) - P(X
 0.7)
0.7)
P(X < 4.3) = P(
 <
<
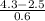 ) = P(Z < 3) = 0.99865
) = P(Z < 3) = 0.99865
P(X
 0.7) = P(
0.7) = P(


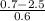 ) = P(Z
) = P(Z
 -3) = 1 - P(Z < 3)
-3) = 1 - P(Z < 3)
= 1 - 0.99865 = 0.00135
Therefore, P(0.7 < X < 4.3) = 0.99865 - 0.00135 = 0.9973
This means that in this interval we are able to find approximately 99.73% of all GPA's for students at this college.
From all these it is clear that the interval (1.9 , 3.7) is expected to find approximately 81.5% of all GPA's for students at this college.