Question

A random sample of 20 healthy adults was collected and their body temperatures were measured in degrees Fahrenheit. The data can be found in an excel file Body with variable name Temperature. Do these data give evidence that the true mean body temperature for healthy adults is not equal to the traditional 98.6 degrees Fahrenheit? Test an appropriate hypothesis at 5% level of significance. (50 points total)

Answer 1

Explanation:

Hello!

You need to test the hypothesis that "the average temperature for healthy adults is not equal to 98.6"

The variable of interest is

X: The body temperature of a healthy adult. (Fahrenheit)

And the parameter of interest is the population mean, μ.

The statistic hypotheses are:

H₀: μ = 98.6

H₁: μ ≠ 98.6

α:0.05

Assuming that the variable has a normal distribution you have to use a one-sample t-statistic for this test.

Attached to the answer is the data of body temperature of n=19 healthy adults. Since you didn't copy the raw data for your exercise I'll use this to answer the question.

Using the data the sample mean and standard deviation are:

X[bar]= 98.12

S= 0.69

`t= (X[bar]-Mu)/((S)/(√(n) ) ) ~~t_(n-1)`

`t_(H_0)= (98.12-98.6)/((0.69)/(√(19) ) ) = -3.03`

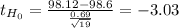
This test is two-tailed, using the critical value approach, you have the rejection region divided into two tails determined by two critical values:

`t_(n-1;\alpha /2)= t_(18;0.025)= -1.965`

`t_(n-1;1-\alpha /2)= t_(18;0.975)= 1.965`

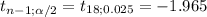
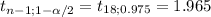
Decision rule:

If
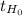`t_(H_0)` ≤ -1.965 or if
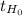`t_(H_0)` ≥ 1.965, the decision is to reject the null hypothesis.

If -1.965 <
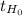`t_(H_0)` < 1.965, the decision is to not reject the null hypothesis.

The calculated statistic is less than the lower critical value, the decision is to reject the null hypothesis.

Using a significance level of 5%, there is enough evidence to reject the null hypothesis. Then you can conclude that the true mean body temperature for healthy adults is not equal to the traditional 98.6F.

I hope this helps!