Question

Drone INC. owns four 3D printers (D1, D2, D3, D4) that print all their Drone parts. Sometimes errors in printing occur. We know that D1, D2, D3, D4 print respectively 15, 25, 40 and 20 percent of the total output of parts. Assume that each of D1, D3, have an error rate of 1 percent while D2, D4 have an error rate of 2 percent. Finally suppose that one printed part is selected randomly from the entire batch and it is found to have an error. Determine the probability that this item is produced by each 3 D printer. Compare the prior probability of D2 with its posterior probability. What is higher prior or posterior probability?

Answer 1

Explanation:

Hello!

There are 4 3D printers available to print drone parts, then be "Di" the event that the printer i printed the drone part (∀ i= 1,2,3,4), and the probability of a randomly selected par being print by one of them is:

D1 ⇒ P(D1)= 0.15

D2 ⇒ P(D2)= 0.25

D3 ⇒ P(D3)= 0.40

D4 ⇒ P(D4)= 0.20

Additionally, there is a chance that these printers will print defective parts. Be "Ei" represent the error rate of each print (∀ i= 1,2,3,4) then:

P(E1)= 0.01

P(E2)= 0.02

P(E3)= 0.01

P(E4)= 0.02

Ei is then the event that "the piece was printed by Di" and "the piece is defective".

You need to determine the probability of randomly selecting a defective part printed by each one of these printers, i.e. you need to find the probability of the part being printed by the i printer given that is defective, symbolically: P(DiIE)

Where "E" represents the event "the piece is defective" and its probability represents the total error rate of the production line:

P(E)= P(E1)+P(E2)+P(E3)+P(E4)= 0.01+0.02+0.01+0.02= 0.06

This is a conditional probability and you can calculate it as:

`P(A/B)= (P(AnB))/(P(B))`

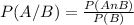
To reach the asked probability, first, you need to calculate the probability of the intersection between the two events, that is, the probability of the piece being printed by the Di printer and being defective Ei.

P(D1∩E)= P(E1)= 0.01

P(D2∩E)= P(E2)= 0.02

P(D3∩E)= P(E3)= 0.01

P(D4∩E)= P(E4)= 0.02

Now you can calculate the probability of the piece bein printed by each printer given that it is defective:

`P(D1/E)= (P(E1))/(P(E)) = (0.01)/(0.06)= 0.17`

`P(D2/E)= (P(E2))/(P(E)) = (0.02)/(0.06)= 0.33`

`P(D3/E)= (P(E3))/(P(E)) = (0.01)/(0.06)= 0.17`

`P(D4/E)= (P(E4))/(P(E)) = (0.02)/(0.06)= 0.33`

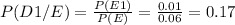
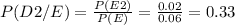
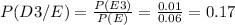
P(D2)= 0.25 and P(D2/E)= 0.33 ⇒ The prior probability of D2 is smaller than the posterior probability.

The fact that P(D2) ≠ P(D2/E) means that both events are nor independent and the occurrence of the piece bein defective modifies the probability of it being printed by the second printer (D2)

I hope this helps!