Question

Mr. Moore is 35 years old today and is beginning to plan for his retirement. He wants to set aside an equal amount at the end of each of the next 25 years so that he can retire at age 60. He expects to live to the maximum age of 80 and wants to be able to withdraw $25,000 per year from the account on his 61st through his 80th birthdays. The account is expected to earn 10% per year (i.e. EAR Determine the size of the annual deposits that must be made by Mr. Moore. a. $212,850 b. $23,449 c. $2,164 d. $8,514

Answer 1

correct option is c. $2,164

Step-by-step explanation:

given data

Cash Flow C = $25000

expected Interest rate r = 10% = 0.10

Total Periods n = 60 year to 80 year = 20 years

solution

we get here present value of ordinary Annuity that is

present value =
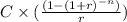`C * (((1-(1+r)^(-n)))/(r))` ....................1

put here value and we get

present value =
`25000* (((1-(1+0.10)^(-20)))/(0.10))`

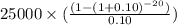
solve it we get

present value = 212839.09

so Annuity paid amount by 35 age to 60 age is $212839.09

and

now it will future value for age 35 year to 60 year that is 25 year time period

Future Value = $212839.09

now we apply formula for future value of ordinary Annuity that is

future value =
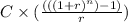`C* (((((1+r)^n)-1))/(r))` ...................2

put here value and we get

$212839.09 =
`c * ((1+0.10)^(25) - 1)/(0.10)`

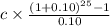
solve it we get

c = $2164.16

so correct option is c. $2,164