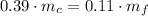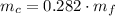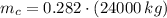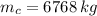Answer:
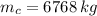
Step-by-step explanation:
According to the Principle of Energy Conservation and the Work-Energy Theorem, the system is modelled as follows:
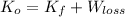 , where
, where
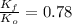 .
.
Then,
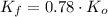
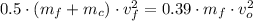
Besides, the Principle of Momentum Conservation describes the following model:
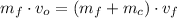
The final velocity of the system is:
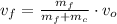
After substituting in the energy expression:
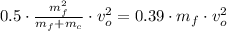
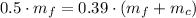
The mass of the caboose is: