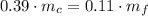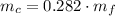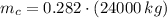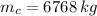Question

A 24000- railroad freight car collides with a stationary caboose car. They couple together, and 22 percent of the initial kinetic energy is dissipated as heat, sound, vibrations, and so on. What is the mass of the caboose

Answer 1

To find the mass of the caboose, we use the principle of conservation of momentum and the fact that 22 percent of the initial kinetic energy is dissipated.

Step-by-step explanation:

To find the mass of the caboose, we can use the principle of conservation of momentum. Since the two cars couple together and move as one, the total momentum before the collision is equal to the total momentum after the collision. The initial momentum of the 24,000-kg freight car can be calculated by multiplying its mass by its velocity (which is not mentioned in the question). Let's assume the initial velocity of the freight car is v. The final velocity of the coupled cars can be calculated by dividing the initial momentum by the total mass (24000 kg + mass of the caboose) of the system. Using the given information that 22 percent of the initial kinetic energy is dissipated, we can also calculate the change in kinetic energy and equate it to 0.78 times the initial kinetic energy. Setting the change in kinetic energy equal to 0.78 times the initial kinetic energy, we can solve for the mass of the caboose.

Answer 2

`m_(c) = 6768\,kg`

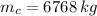
Step-by-step explanation:

According to the Principle of Energy Conservation and the Work-Energy Theorem, the system is modelled as follows:

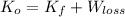`K_(o) = K_(f) + W_(loss)`, where
`(K_(f))/(K_(o)) = 0.78`.

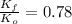Then,

`K_(f) = 0.78\cdot K_(o)`

`0.5\cdot (m_(f)+m_(c))\cdot v_(f)^(2) = 0.39\cdot m_(f)\cdot v_(o)^(2)`

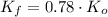
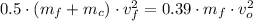
Besides, the Principle of Momentum Conservation describes the following model:

`m_(f)\cdot v_(o) = (m_(f)+m_(c))\cdot v_(f)`

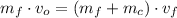
The final velocity of the system is:

`v_(f) = (m_(f))/(m_(f)+m_(c))\cdot v_(o)`

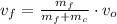
After substituting in the energy expression:

`0.5\cdot (m_(f)^(2))/(m_(f)+m_(c))\cdot v_(o)^(2) = 0.39\cdot m_(f)\cdot v_(o)^(2)`

`0.5\cdot m_(f) = 0.39\cdot (m_(f)+m_(c))`

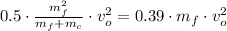
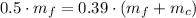
The mass of the caboose is:

`0.39\cdot m_(c) = 0.11\cdot m_(f)`

`m_(c) = 0.282\cdot m_(f)`

`m_(c) = 0.282\cdot (24000\,kg)`

`m_(c) = 6768\,kg`