Question

A bullet of mass 2.6 g strikes a ballistic pendulum of mass 3.6 kg. The center of mass of the pendulum rises a vertical distance of 13 cm. Assuming that the bullet remains embedded in the pendulum, calculate the bullet's initial speed.

Answer 1

2211.4 m/s

Step-by-step explanation:

We are given that

Mass of bullet,m=2.6 g=
`2.6* 10^(-3) kg`

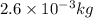
1 kg=
`10^3 g`

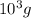
Mass of pendulum,M=3.6 kg

Vertical distance,y=13 cm=
`(13)/(100)=0.13 m`

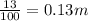
1 m=100 cm

We have to find the bullet's initial speed.

Kinetic energy of bullet=P.E

`(1)/(2)(M+m)v^2=(m+M)gh`

`v^2=2gh`

`v=√(2gh)`

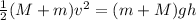
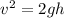
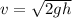
Where
`g=9.8 m/s^2`

`v=√(2* 9.8* 0.13)=1.596m/s`

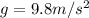
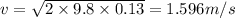
According to law of conservation of momentum

`mu=(m+M)v`

`u=(m+M)/(m)v`

`u=(2.6* 10^(-3)+3.6)/(2.6* 10^(-3))* 1.596`

`u=2211.4 m/s`

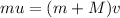
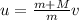
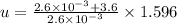
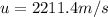
Hence, the bullet's initial speed=2211.4 m/s