Answer:
2211.4 m/s
Step-by-step explanation:
We are given that
Mass of bullet,m=2.6 g=

1 kg=

Mass of pendulum,M=3.6 kg
Vertical distance,y=13 cm=
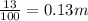
1 m=100 cm
We have to find the bullet's initial speed.
Kinetic energy of bullet=P.E

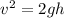
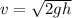
Where


According to law of conservation of momentum
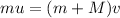
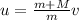
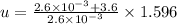
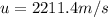
Hence, the bullet's initial speed=2211.4 m/s