Answer:
The computations are shown below:
Step-by-step explanation:
a. The computation of the economic order quantity is shown below:

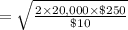
= 1,000 units
The carrying cost is
= $40 × 25%
= $10
b. The number of orders would be equal to
= Annual demand ÷ economic order quantity
= $20,000 ÷ 1,000 units
= 20 orders
The average inventory would equal to
= Economic order quantity ÷ 2
= 1,000 units ÷ 2
= 500 units
d. The total cost of ordering cost and carrying cost equals to
Ordering cost = Number of orders × ordering cost per order
= 20 orders × $250
= $5,000
Carrying cost = average inventory × carrying cost per unit
= 500 units × $10
= $5,000
So, the total would be
= $5,000 + $5,000
= $10,000