Question

ASK YOUR TEACHER A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 4 ft/s along a straight path. How fast is the tip of his shadow moving when he is 50 ft from the pole?

Answer 1

Tip of the shadow is moving at the rate of
`(20)/(3)\:ft/s`.

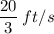Explanation:

Refer to the attachment.

Let AB be the height of the street light. So, AB = 15 ft.

Let DE be the height of the man. So, DE = 6 ft.

Let BE be the distance between the man and light pole. Assume BE = x

Let BC be the distance between tip of shadow and light pole. Assume BC = y

Now height of the shadow of the man is EC which can be calculated as follows,

BC = BE + EC

y = x + EC

Subtracting x,

y – x = EC.

So there are two triangles that is, triangle ABC and triangle DEC. Assume that both the triangles are similar.

So applying similar triangle property,

`(AB)/(BC)=(DE)/(EC)`

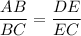
Substituting the value,

`(15)/(y)=(6)/(y-x)`

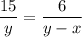
Cross multiplying,

`15* \left(y-x\right)=6* y`

Using distributive property,

`15y-15x=6y`

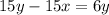
Subtracting 6y,

`15y-6y-15x=0`

Adding 15x,

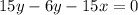
`15y-6y=15x`

`9y=15x`

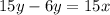
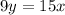
Dividing by 9,

`y=(15)/(9)x`

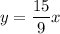
Multiply and divide by 3,

`y=(5)/(3)x`

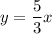
Differentiating above equation with respect to t,

`(dy)/(dt)=(d)/(dt)\left((5)/(3)x\right)`

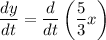
Applying constant multiple rule,

`(dy)/(dt)=(5)/(3)(d)/(dt)\left(x\right)`

`(dy)/(dt)=(5)/(3)(dx)/(dt)`

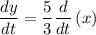
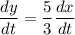
Given that man walks away from the pole with a speed of 4 ft/s that is,

`(dx)/(dt)=4`

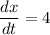
Substituting the value,

`(dy)/(dt)=(5)/(3)\left(4\right)`

`(dy)/(dt)=(20)/(3)\:ft/s`

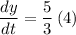
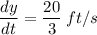
Therefore, tip of the shadow is moving at the rate of
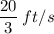`(20)/(3)\:ft/s`.