Question

A firm has an issue of $1,000 par value bonds with a 9 percent stated interest rate outstanding. The issue pays interest annually and has 20 years remaining to its maturity date. If bonds of similar risk are currently earning 11 percent, the firm's bond will sell for ________ today.

Answer 1

$841 approx

Step-by-step explanation:

Bonds refer to debt instruments whereby the issuer raises long term finance, agreeing to pay the lenders, a fixed rate of coupon payments at regular intervals and repayment of principal upon maturity.

The present value of a bond is represented as:

`B_(0) = (C)/((1\ +\ K)^(1) ) \ +\ (C)/((1\ +\ K)^(2) ) \ +\ ....(C)/((1\ +K)^(n) )\ +\ (RV)/((1\ +\ K)^(n) )`

where
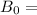`B_(0) =` Present value of a bond

C = Annual coupon payments

k = yield to maturity/ cost of debt

n = years to maturity

RV = Redemption value

here, C = 1000 × 9% = $90

K = 11%

n = 20 years

RV = $1000

putting these values in the above equation, we have,

`B_(0) = (90)/((1\ +\ .11)^(1) ) \ +\ (90)/((1\ +\ .11)^(2) ) \ +\ ....(90)/((1\ +.11)^(20) )\ +\ (1000)/((1\ +\ .11)^(20) )`

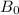`B_(0)` = 7.9633 × 90 + 0.124 × 1000

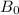`B_(0)` = 716.699 + 124.033

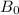`B_(0)` = $ 840.73 OR $ 841 approx.

Thus, the bond will sell at $841 today.