Question

Calculate the maximum solubility of silver carbonate, Ag2CO3 in g/L when in the presence of 0.057 M AgNO3. The solubility product of Ag2CO3 is 8.1x10-12 and Ag2CO3 has a molar mass of 167.91 g/mol. Express your answer to the correct number of significant figures, in scientific notation and include units with your answer.

Answer 1

Approximately
`4.2 * 10^(-7)\; \rm g \cdot L^(-1)`.

Step-by-step explanation:

Start by finding the concentration of
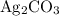`\rm Ag_2CO_3` at equilibrium. The solubility equilibrium for

`\rm Ag_2CO_3 \; (s) \rightleftharpoons 2\, Ag^(+)\; (aq) + {CO_3}^(2-)\; (aq)`.

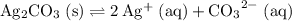The ratio between the coefficient of
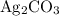`\rm Ag_2CO_3` and that of
`\rm Ag^(+)` is
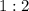`1:2`. For

Let the increase in
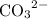`\rm {CO_3}^(2-)` concentration be
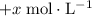`+x\; \rm mol \cdot L^(-1)`. The increase in
`\rm Ag^(+)` concentration would be
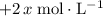`+2\,x\; \rm mol \cdot L^(-1)`. Note, that because of the
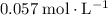`0.057\; \rm mol \cdot L^(-1)`of
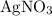`\rm AgNO_3`, the concentration of

• The concentration of
  `\rm Ag^(+)` would be
  `(0.057 + 2\, x) \; \rm mol\cdot L^(-1)`.
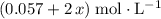• The concentration of
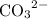  `\rm {CO_3}^(2-)` would be
  `x\; \rm mol \cdot L^(-1)`.

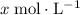Apply the solubility product expression (again, note that in the equilibrium, the coefficient of
`\rm Ag^(+)` is two) to obtain:

`\begin{aligned}&\rm \left[Ag^(+)\right]^2 \cdot \left[{CO_3}^(2-)\right] = K_{\text{sp}} \\ & \implies (0.057 + x)^2\cdot x = 8.1 * 10^(-12) \end{aligned}`.

Note, that the solubility product of
`\rm Ag_2CO_3`,
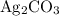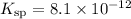`K_{\text{sp}} = 8.1 * 10^(-12)` is considerably small. Therefore, at equilibrium, the concentration of

Apply this approximation to simplify
`(0.057 + x)^2\cdot x = 8.1 * 10^(-12)`:

`0.057^2\, x \approx (0.057 + x)^2 \cdot x = 8.1 * 10^(-12)`.

`\begin{aligned} x &\approx (8.1 * 10^(-12))/(0.057^2)\end{aligned}`.

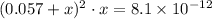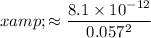Calculate solubility (in grams per liter solution) from the concentration. The concentration of
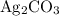`\rm Ag_2CO_3` is approximately
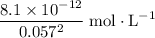`\displaystyle (8.1 * 10^(-12))/(0.057^2)\; \rm mol\cdot L^(-1)`, meaning that there are approximately
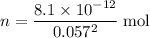`\displaystyle n = (8.1 * 10^(-12))/(0.057^2)\; \rm mol` of

`\begin{aligned}m &= n \cdot M \\ &\approx \displaystyle (8.1 * 10^(-12))/(0.057^2) \; \rm mol* 167.91\; g \cdot mol^(-1) \\ &\approx 4.2 * 10^(-7)\; \rm g \end{aligned}`.

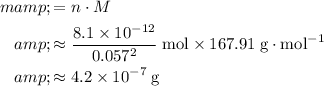As a result, the maximum solubility of
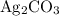`\rm Ag_2CO_3` in this solution would be approximately
`4.2 * 10^(-7)\; \rm g \cdot L^(-1)`.