Question

A circle with area 9pi has a sector with a central angle of 17/9pi radians. What is the area of the sector?

Answer 1

Given:

The circle has an area of 9π

The area of the shaded region has a central angle of
`(17)/(9) \pi`

We need to determine the area of the shaded region.

Area of the shaded region:

The section of the circle that is shaded is given by

`((17)/(9) \pi)/(2 \pi)=(17 \pi)/(18 \pi)`

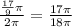
Simplifying, we get;

`(17)/(18)`

Thus, the section of the circle that is shaded is
`(17)/(18)`

Area of the shaded region is given by

`A=9 \pi \cdot (17)/(18)`

`A=8.5 \pi`

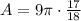
Thus, the area of the shaded region is 8.5π