Question

Light rays in a material with index of refrection 1.29 1.29 can undergo total internal reflection when they strike the interface with another material at a critical angle of incidence. Find the second material's index of refraction n n when the required critical angle is 65.9 ∘ .

Answer 1

The second material's index of refraction is 1.17.

Step-by-step explanation:

Given that,

Refractive index of the material, n = 1.29

Critical angle is 65.9 degrees.

We need to find the second material's index of refraction. We know that at critical angle of incidence, angle of refraction is equal to 90 degrees. Using Snell's law as:

`n_1\sin \theta_c=n_2\sin (90)\\\\n_2=n_1\sin \theta_c\\\\n_2=1.29* \sin (65.9)\\\\n_2=1.17`

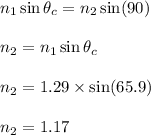
So, the second material's index of refraction is 1.17.