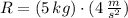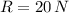Question

A 3.0-kg and a 5.0-kg box rest side-by-side on a smooth, level floor. A horizontal force of 32 N is applied to the 3.0-kg box pushing it against the 5.0-kg box, and, as a result, both boxes slide along the floor. How large is the contact force between the two boxes

Answer 1

`R = 20\,N`

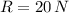
Step-by-step explanation:

The free body diagrams of each box are presented in the images attached below. Given the smoothness of the level floor, friction forces can be neglected and due to the contact (3rd Newton's Law) betweeen each other, both boxes experiment the same acceleration:

Box A

`\Sigma F_(x) = F - R = m_(A)\cdot a`

`\Sigma F_(y) = N_(A) - m_(A)\cdot g = 0`

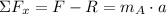
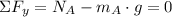
Box B

`\Sigma F_(x) = R = m_(B)\cdot a`

`\Sigma F_(y) = N_(B) - m_(B)\cdot g = 0`

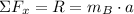
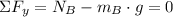
After some algebraic manipulation:

`F = (m_(A) + m_(B))\cdot a`

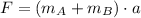
The acceleration experiment for each box is:

`a = (F)/(m_(A)+m_(B))`

`a = (32\,N)/(3\,kg + 5\,kg)`

`a = 4\,(m)/(s^(2))`

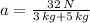
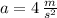
The contact between the two boxes is:

`R = (5\,kg)\cdot (4\,(m)/(s^(2)))`

`R = 20\,N`