Question

The temperature of coffee served at a restaurant is normally distributed with an average temperature of 160 degrees Fahrenheit and a standard deviation of 5.4 degrees Fahrenheit. What is the coffee temperature for the 20th percentile? Enter your answer to four decimal places.

Answer 1

The 20th percentile of coffee temperature is 155.4532 degrees Fahrenheit.

Explanation:

We are given the following information in the question:

Mean, μ = 160 degrees

Standard Deviation, σ = 5.4 degrees

We are given that the distribution of temperature of coffee is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

We have to find the value of x such that the probability is 0.2

`P( X < x) = P( z < \displaystyle(x - 160)/(5.4))=0.2`

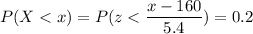
Calculation the value from standard normal z table, we have,

`\displaystyle(x - 160)/(5.4) = -0.842\\\\x = 155.4532`

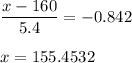
Thus,

`P_(20)=155.4532`

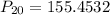
The 20th percentile of coffee temperature is 155.4532 degrees Fahrenheit.