Answer:
0.139
Explanation:
We are given that
Total number of cards=52
n=18
We have to find the probability of drawing at least 7 spades
Total number of spaded in deck of 52 cards=13
Probability of getting spade=
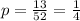
Probability,
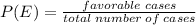
Probability of getting no spade=
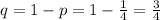
By binomial theorem of probability
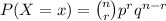
P(x

The probability of drawing at least 7 spades=
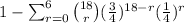
The probability of drawing at least 7 spades=0.139