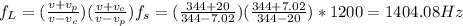Question

Unless indicated otherwise, assume the speed of sound in air to be v = 344 m/s. A stationary police car emits a sound of frequency 1200 Hz that bounces off a car on the highway and returns with a frequency of 1250 Hz. The police car is right next to the highway, so the moving car is traveling directly toward or away from it. (a) How fast was the moving car going? Was it moving toward or away from the police car? (b) What frequency would the police car have received if it had been traveling toward the other car at 20.0 m/s?

Answer 1

a) The velocity of the car is 7.02 m/s and the car is approaching to the police car as the frequency of the police car is increasing.

b) The frequency is 1404.08 Hz

Step-by-step explanation:

If the police car is a stationary source, the frequency is:

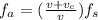`f_(a) =((v+v_(c) )/(v) )f_(s)` (eq. 1)

fs = frequency of police car = 1200 Hz

fa = frequency of moving car as listener

v = speed of sound of air

vc = speed of moving car

If the police car is a stationary observer, the frequency is:

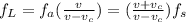`f_(L) =f_(a) ((v)/(v-v_(c) ) )=((v+v_(c) )/(v-v_(c) ) )f_(s)` (eq. 2)

Now,

fL = frequecy police car receives

fs = frequency police car as observer

a) The velocity of car is from eq. 2:

`1250=1200((v+v_(c) )/(v-v_(c) ) )\\1250(v-v_(c) )=1200(v+v_(c) )\\v_(c) =(50*344)/(2450) =7.02m/s`

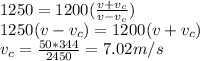
b) Substitute eq. 1 in eq. 2:

`f_(L) =((v+v_(p) )/(v-v_(c) ) )((v+v_(c) )/(v-v_(p) ) )f_(s) =((344+20)/(344-7.02) )((344+7.02)/(344-20) )*1200=1404.08Hz`