Question

A data analyst wants to set up a hypothesis test to determine if the mean number of courses taken in a college semester is different for freshmen, versus sophomores, versus juniors, versus seniors. Label these four groups of students as years 1, 2, 3, and 4. What would be the correct setup for the null and alternative hypotheses for this test? Select the correct answer below: H0:μ1=μ2=μ3 Ha: at least one of the means is different H0:μ1=μ2=μ3=μ4 Ha: at least one of the means is different H0: at least one of the means is different Ha:μ1=μ2=μ3=μ4

Answer 1

Null hypothesis:
`\mu_(1)=\mu_(2)=\mu_(3)= \mu_(4)`

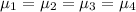
Alternative hypothesis: Not all the means are equal
`\mu_(i)\\eq \mu_(j), i,j=1,2,3,4`

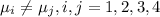
The best option for this case would be:

H0:μ1=μ2=μ3=μ4

Ha: at least one of the means is different

Explanation:

Previous concepts

Analysis of variance (ANOVA) "is used to analyze the differences among group means in a sample".

The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"

Solution to the problem

For this case we are trying to proof if the mean number of courses taken in a college semester is different for freshmen, versus sophomores, versus juniors, versus seniors.

Based on this case we can set up the following system of hypothesis:

Null hypothesis:
`\mu_(1)=\mu_(2)=\mu_(3)= \mu_(4)`

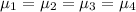
Alternative hypothesis: Not all the means are equal
`\mu_(i)\\eq \mu_(j), i,j=1,2,3,4`

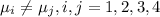
The best option for this case would be:

H0:μ1=μ2=μ3=μ4

Ha: at least one of the means is different