Question

Suppose that the weight of seedless watermelons is normally distributed with mean 6.2 kg. and standard deviation 1.5 kg. Let X be the weight of a randomly selected seedless watermelon. Round all answers to two decimal places.

A. X ~ N(___ , ____ )

B. What is the median seedless watermelon weight?____ kg.

C. What is the Z-score for a seedless watermelon weighing 8 kg?

D. What is the probability that a randomly selected watermelon will weigh more than 7 kg?

E. What is the probability that a randomly selected seedless watermelon will weigh between 4 and 5 kg?

F. The 80th percentile for the weight of seedless watermelons is _____ kg.

Answer 1

A.

• X ~ N(6.2kg, 2.25kg²)

B. What is the median seedless watermelon weight?____ kg.

• 6.2 kg

C. What is the Z-score for a seedless watermelon weighing 8 kg?

• 1.2

D. What is the probability that a randomly selected watermelon will weigh more than 7 kg?

• 0.2981

E. What is the probability that a randomly selected seedless watermelon will weigh between 4 and 5 kg?

• 0.1411

F. The 80th percentile for the weight of seedless watermelons is _____ kg.

• 7.5 kg

Step-by-step explanation:

A. X ~ N(___ , ____ )

The distribution of a random variable in a sample extracted from a population that follows a normal distribution is represented by the notation:

• X ~ N(μ, σ²)

Where:

• X is the random variable
• N stands for normal distribution function
• μ is the median of the population
• σ² is the variance of the population

Here, you have:

• μ = 6.2 kg

• σ² = (1.5kg)² = 2.25 kg²

• X ~ N(6.2kg, 2.25kg²)

B. What is the median seedless watermelon weight?____ kg.

The median of a random variable that follows a normal distribution is equal to the mean, thus it is 6.2 kg.

C. What is the Z-score for a seedless watermelon weighing 8 kg?

The z-score is the standardized value of the random variable. It measures how far away is the variable from the mean.

It is calcuated with the formula:

`Z-score(X=x)=(x-\mu)/(\sigma)`

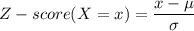
Thus for X=8:

`Z(X=8)=(8-6.2)/(1.5)=1.2`

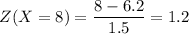
D. What is the probability that a randomly selected watermelon will weigh more than 7 kg?

You want P(X>7)

You must use the tables for the standardized normal distribution.

Find the corresponding Z-score for X = 7

`Z(X=7)=(7-6.2)/(1.5)\approx0.53`

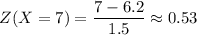
You must use a table for the standardized normal distribution which gives the cumulative distribution or area under the curve of the standard normal distribution and find P(Z>0.53).

That is the area to the right of Z=0.53. The table shows 0.2981.

Thus, the probability that a randomly selected seedless watermelon will weigh more than 7 kg is 0.2981

E. What is the probability that a randomly selected seedless watermelon will weigh between 4 and 5 kg?

For this case you must find the Z-scores for X=4 and X=5 and then find the area under the curve of the standardized normal distribution between those two Z-scores.

• Z(X=4) = (4 - 6.2)/1.5 ≈ -1.47

• Z(X=5) = (5 - 6.2)/1.5 = -0.8

In the table the area to the right of Z = - 1.47 is 1 - 0.0708 = 0.9292

And the area to the right of Z = - 0.8 is 1 - 0.2119 = 0.7881

Thus, the area in between is the difference 0.9292 - 0.7881 = 0.1411.

F. The 80th percentile for the weight of seedless watermelons is _____ kg.

The 80th percentile is the weigh of the top 20% seedless watermelons: this is 80% of the weighs are below that weight.

You must find the Z-score for which the area under the curve is less than 0.80.

The area less than 0.80 is 1 less the area that is less than 0.20.

From the table, the Zscore that defines the area less than 0.20 is 0.845 (interpolating).

Thus, the 80th percentile is the X value that makes the Z-score greater than or equal to 0.845:

• Z ≥ 0.845

• (X - 6.2)/1.5 ≥ 0.845

• X ≥ 0.845 × 1.5 + 6.2

• X ≥ 7.4675

• X ≥ 7.5 kg ← answer