Question

1. Suppose you would like to build a parking lot next adjacent to your office building: For insurance reasons, assume that you are required to put a fence around all sides of the lot except for the one touching the building. What is the largest (in terms of surface area) parking lot that you can surround with 6,000 feet of fence

Answer 1

4,500,000 ft²

Step-by-step explanation:

Let 'x' be the length of the side parallel to the building, and 'y' be length of each of the sides perpendicular to the building. The area function (A) can be written as a function of 'y' as follows:

`x+2y=6,000\\x=6,000-2y\\A(x,y) = xy\\A(y) = (6,000-2y)*y\\A(y) = -2y^2+6,000y`

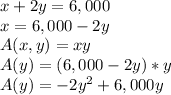
The value of 'y' for which the derivate of the area function is zero, is length that maximizes the area:

`A(y) = -2y^2+6,000y\\A'(y) = -4y+6,000\\y=1,500\ ft\\A(1500) = -2*(1,500)^2+6,000*1,500\\A_(max)=4,500,000\ ft^2`

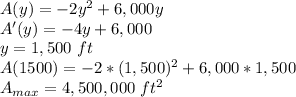
The largest parking lot possible has an area of 4,500,000 ft².