Question

A main-sequence star of 3 solar masses has a radius of approximately 2.5 times the radius of our Sun. According to Newton’s formula, what would happen to the gravitational force felt by an object on the surface of this 3-solar-mass star if the star’s entire mass gradually collapsed to a singularity? Assume the object remains on the surface of the star throughout the collapse.

Answer 1

The gravitational force on the object would gradually increase toward infinity.

Step-by-step explanation:

Given:

Mass of the main-sequence star = 3M ...where
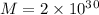`M=2* 10^3^0` kg

Radius of the star = 2.5R ...where
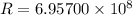`R=6.95700* 10^8` m

According to the question:

The entire star mass gradually collapse to a singularity.

Using Newtons law we have to find the gravitational force.

⇒ Gravitational force,
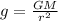`g=(GM)/(r^2)` ..equation (i)

From the above equation we can say that mass is in direct proportion whereas radius is inverse proportion of the gravitational force.

Note:

Whenever any star's mass collapsed to singularity, virtually in mathematical term the volume of the star is said to be zero and its density becomes infinite.

Density infinite means mass infinite as
`\rho = (m)/(V)` .

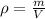Now:

As mass or the density tends to infinity,then gravitational force also tends to infinity.

Mathematically:

Lets take the mass as one unit then and radius as 'x'.

As the radius will shrink to zero.

⇒
`\lim_(x \to 0) (1)/(x) = (1)/(0) = \infty`

So

The gravitational force on the object would gradually increase toward infinity.