Question

The mean birth weight of a sample of 195 boys is 32.7 hg with standard deviation 6.6 hg. Give the lower and upper endpoints of a 95% confidence interval for the mean birth weight of all boys. Round your answer to one decimal place.

Answer 1

Lower end point = 31.8 hg

Upper end point = 33.7 hg

Explanation:

We are given the following in the question:

Sample mean,
`\bar{x}` = 32.7 hg

Sample size, n = 195

Alpha, α = 0.05

Standard deviation, s = 6.6 hg

Degree of freedom = n - 1 = 194

95% Confidence interval:

`\bar{x} \pm t_(critical)\displaystyle(s)/(√(n))`

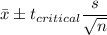
Putting the values, we get,

`t_(critical)\text{ at degree of freedom 194 and}~\alpha_(0.05) = \pm 1.972`

`32.7 \pm 1.972((6.6)/(√(195)) )\\\\ = 32.7 \pm 0.932\\ = (31.768 ,33.632)\\\approx (31.8,33.7)`

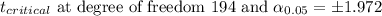
Lower end point = 31.8 hg

Upper end point = 33.7 hg