Question

Gravel is being dumped from a conveyor belt at a rate of 40 ft3/min, and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal. How fast is the height of the pile increasing when the pile is 11 ft high

Answer 1

The height is increasing at the rate of 0.42 ft/min

Explanation:

Given that:

The diameter = height

and

diameter d = 2 r

2 r = h

r =
`(h)/(2)`

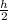
The volume of the cone formed = v

v ⇒
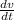`(dv)/(dt)` = 40 ft³/ min

`v = (1)/(3) \pi r^2h`

`v = (1)/(3) \pi ((h)/(2))^2 h`

`v = (1)/(3) \pi (h^3)/(4)`

`v = (\pi)/(12)h^3`

`(dv)/(dt)= (\pi)/(12)3h^2(dh)/(dt)`

`(dv)/(dt)= (\pi)/(4)h^2(dh)/(dt)`

`(dh)/(dt)= (4)/(\pi h^2)(dv)/(dt)`

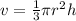
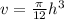
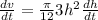
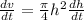
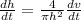
at h = 11 ft high

`(dh)/(dt)= (4)/(\pi (11)^2)* (40)`

`(dh)/(dt)= 0.42 \ ft/min`

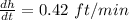
Hence, the height of the pile was increasing at the rate of 0.42 ft/min