Question

An open top box is constructed from a rectangular sheet of material by cutting equal squares from each corner and folding up the edges. If the sheet of material measures 15 inches by 11 inches, find the dimensions of the box so that the volume is maximized.

Answer 1

Therefore the dimensions of the box is 10.82 inches × 6.82 inches ×2.09 inches.

Explanation:

Given that, by cutting equal squares from each corner form a rectangular sheet of material, an open top box is constructed.

The dimensions of the material is 15 inches by 11 inches.

Assume that,the side of the square be x.

The length of the box is= (15 -2x) inches

The width of the box is =(11-2x) inches

The height of the box is = x inches.

The volume of the box is = Length× width×height

=(15-2x)(11-2x)x cubic inches

=(165-52x+4x²)x cubic inches

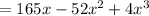`=165x -52x^2+4x^3` cubic inches

Let,

V
`=165x -52x^2+4x^3`

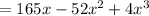
Differentiating with respect to x

V'=
`165-104x+12x^2`

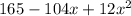
Again differentiating with respect to x

V''= -104 +24x

Now, we set V'=0

`165-104x+12x^2=0`

`\Rightarrow x=(-(-104)\pm√((-104)^2-4.12.165))/(2.12)`

`\Rightarrow x=(104\pm √(2896))/(24)`

`\Rightarrow x=(104\pm 4√(181))/(24)`

`\Rightarrow x= 2.09,6.58`

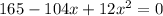
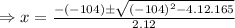
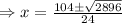
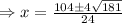
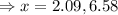
For x=6.58 the width of the box will be negative.

∴x=2.09

`V''|_(x=2.09)=-104+(24* 2.09)=-5384<0`

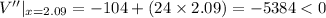
Since V''<0 at x= 2.09,

Therefore V is maximum when x=2.09.

The length of the box is = {15-(2×2.09)}=10.82 inches

The width of the box is ={11-(2×2.09)}=6.82 inches

The height of the box is 2.09 inches.

Therefore the dimensions of the box is 10.82 inches × 6.82 inches ×2.09 inches.