Question

A rifle with a weight of 25 N fires a 4.5-g bullet with a speed of 240 m/s. (a) Find the recoil speed of the rifle. m/s (b) If a 650-N man holds the rifle firmly against his shoulder, find the recoil speed of the man and rifle.

Answer 1

The recoil speed of the man and rifle is
`v_(man)=0.016 ms^(-1)`.

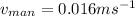Step-by-step explanation:

The expression for the force in terms of mg is as follows;

F=mg

Here, m is the mass and acceleration due to gravity.

Rearrange the expression for mass.

`m=(F)/(g)`

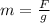
Calculate the combined mass of the man and rifle.

`m_(man,rifle)=(650+25)/(g)`

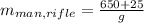
Put
`g=9.8 ms^(-2)`.

`m_(man,rifle)=(650+25)/(9.8)`

`m_(man,rifle)=68.88 kg`

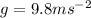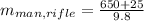
The expression for the conservation of momentum is as follows as;

`m_(man)u_(man)+m_(bullet)u_(bullet)=m_(man)v_(man)+m_(rifle)v_(man,rifle)`

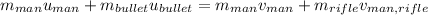
Here,
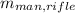`m_(man,rifle)` is the mass of the man and rifle,
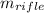`m_(rifle)` is the mass of the rifle,
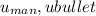`u_(man),u{bullet}` are the initial velocities of the man and bullet and
`v_(man),v{man,rifle}` are the final velocities of the man and rifle and rifle.

It is given in the problem that a rifle with a weight of 25 N fires a 4.5-g bullet with a speed of 240 m/s.

Convert mass of rifle from gram to kilogram.

`m_(bullet)=4.5 g`

`m_(bullet)=.0045 kg`

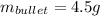
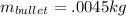
Put
`m_(bullet)=.0045 kg`,
`m_(man,rifle)=68.88 kg` ,
`u_(man,rifle)=0`,
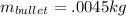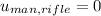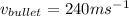`v_(bullet)= 240 ms^(-1)` and
`u_(bullet)=0`.

`m_(man)(0)+m_(bullet)(0)=(68.88)v_(man,rifle)+(.0045)(240)`

`0=(68.88)v_(man,rifle)+(.0045)(240)`

`0=(68.88)v_(man,rifle)+1.08`

`(68.88)v_(man,rifle)=(-1.08)/(68.88)`

`v_(man,rifle)=-0.016 ms^(-1)`

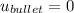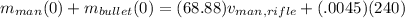
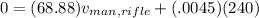
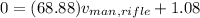
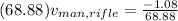
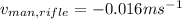
Therefore, the recoil speed of the man and rifle is
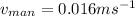`v_(man)=0.016 ms^(-1)`.