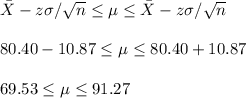Question

How much does a sleeping bag cost? Let's say you want a sleeping bag that should keep you warm in temperatures from 20°F to 45°F. A random sample of prices ($) for sleeping bags in this temperature range is given below. Assume that the population of x values has an approximately normal distribution. 50 80 95 70 100 40 30 23 100 110 105 95 105 60 110 120 95 90 60 70a) Use a calculator with mean and sample standard deviation keys to find the sample mean price x and sample standard deviation s. (Round your answers to two decimal places.)

x =
s =
(b) Using the given data as representative of the population of prices of all summer sleeping bags, find a 90% confidence interval for the mean price μ of all summer sleeping bags. (Round your answers to two decimal places.)
lower limit
upper limit

Answer 1

a) x = 80.40

s = 29.54

b) lower limit = 69.53

upper limit = 91.27

Explanation:

The mean price is:

`\bar X=(1)/(n)\sum x_i=(1)/(20)(50+80+...+70)=(1608)/(20) =80.40`

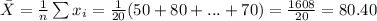
The standard deviation is

`s=\sqrt{(1)/(n-1)\sum(x_i-\bar X)^2}=\sqrt{(1)/(19)[(50-80.4)^2+...+(70-80.4)^2]} \\\\s=\sqrt{(15,471)/(19) }=√(814.25) =29.54`

We have to calculate a 90% CI for the mean.

The z-value for a 90% confidence interval is z=1.645.

The margin of error is:

`E=z\cdot \sigma / √(n)=1.645*29.54/√(20)=48.59/4.47=10.87`

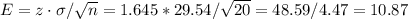
The 90% CI is

`\bar X-z\sigma/√(n) \leq \mu \leq \bar X-z\sigma/√(n)\\\\80.40-10.87 \leq \mu \leq 80.40+10.87\\\\69.53\leq \mu \leq 91.27`