Answer:
Therefore the constant angular acceleration of the wheel 12.43 rad /s².
Step-by-step explanation:
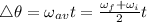
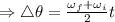
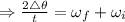
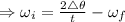
and
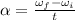
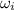 = initial angular velocity
= initial angular velocity
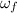 = final angular velocity
= final angular velocity
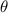 = displacement
= displacement
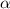 = angular acceleration
= angular acceleration
t = time
Here
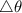 = 37.0 revolution
= 37.0 revolution
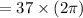 rad [ since one revolution =
rad [ since one revolution =
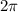 ]
]
t=2.92 s
Final angular velocity =
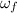 = 97.8 rad/s
= 97.8 rad/s
To find the angular velocity, first we need to find out the initial angular velocity
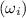 .
.
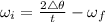
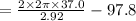
= 61.50 rad /s
Then the angular velocity is
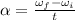
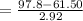 rad /s²
rad /s²
=12.43 rad /s²
Therefore the constant angular acceleration of the wheel 12.43 rad /s².