Question

ASK YOUR TEACHER A rotating wheel requires 2.92-s to rotate through 37.0 revolutions. Its angular speed at the end of the 2.92-s interval is 97.8 rad/s. What is the constant angular acceleration of the wheel

Answer 1

Therefore the constant angular acceleration of the wheel 12.43 rad /s².

Step-by-step explanation:

`\triangle \theta =\omega_(av)t=(\omega_f+\omega_i)/(2)t`

`\Rightarrow \triangle \theta =(\omega_f+\omega_i)/(2)t`

`\Rightarrow (2\triangle \theta)/(t) ={\omega_f+\omega_i}`

`\Rightarrow {\omega_i= (2\triangle \theta)/(t) -\omega_f}`

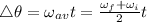
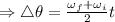
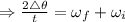
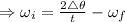
and

`\alpha =(\omega_f-\omega_i)/(t)`

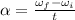
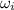`\omega_i` = initial angular velocity

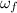`\omega_f` = final angular velocity

`\theta` = displacement

`\alpha` = angular acceleration

t = time

Here
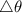`\triangle \theta` = 37.0 revolution
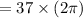`=37 *(2\pi)` rad [ since one revolution =
`2 \pi`]

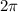t=2.92 s

Final angular velocity =
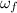`\omega_f` = 97.8 rad/s

To find the angular velocity, first we need to find out the initial angular velocity
`(\omega_i)`.

`{\omega_i= (2\triangle \theta)/(t) -\omega_f}`

`=(2*2\pi * 37.0)/(2.92)-97.8`

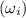= 61.50 rad /s

Then the angular velocity is

`\alpha =(\omega_f-\omega_i)/(t)`

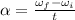
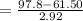`=(97.8-61.50)/(2.92)` rad /s²

=12.43 rad /s²

Therefore the constant angular acceleration of the wheel 12.43 rad /s².