Question

A 12.0 kg mass, fastened to the end of an aluminum wire with an unstretched length of 0.50 m, is whirled in a vertical circle with a constant angular speed of 120 rev/min. The cross-sectional area of thewire is 0.014 cm2. Calculate the elongation of the wire when the mass is a) at its lowest point of the path and b) at the highest point of its path

Answer 1

a) the elongation of the wire when the mass is at its lowest point on the path = 0.5 cm

b) the elongation of the wire when the mass is at its highest point on the path = 0.42 cm

Step-by-step explanation:

Given that;

the angular speed
`\omega = 120 \ rev/min`

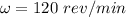
Then converting it to rad/s ; we have:

=
`(120 \ rev/min )((2 \ \pi \ rad )/(1 \ rev) ) ((1 \ min )/(60 \ s) )`

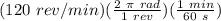
= 12.57 rad/s

The cross-sectional area of the wire A = 0.014 cm²

A = (0.014 cm²) (
`(10^(-4) \ m^2)/(1 \ cm^3)`)

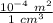A =
`0.014*10^(-4) \ m^2`

mass (m) = 12.0 kg

R = 0.5 m

g = 9.8 m/s²

To calculate for the mass when its at the lowest point of the path; we use the Newton's second law of motion; which is expressed as:

`T - mg = ma_(rad)`

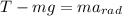
where;

`a_rad = ( radical \ acceleration ) = R \omega^2`

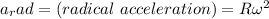
Now; we can rewrite our equation as;

`T -mg = m R \omega ^2`

`T = mR \omega^2 + mg`

`T = m( R \omega^2 + g)`

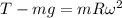
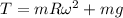
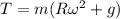
Replacing our given values ; we have:

`T = 12.0( 0.5(12.57)^2 + 9.8)`

`T = 12.0( 0.5(158.0049) + 9.8)`

`T = 12.0( 79.00245 + 9.8)`

`T = 12.0( 88.80245)`

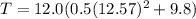
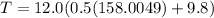
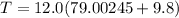
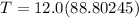
T = 1065.6294 N

T ≅ 1066 N

Determining the elongation
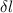`\delta l` in the wire by using the equation

Y =
`(Tl)/(AY)`

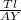
Making
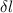`\delta l` the subject of the formula; we have

`\delta l = (Tl)/(AY)`

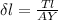
where ;

l = length of the wire

T =Tension in the wire

A = cross - sectional area

Y = young's modulus

Then;

`\delta l = ((1066 N)(0.5m))/((0.014*10^(-4)m^2)(7.0*10^(10)Pa))`

`\delta l` =
`( 0.00544 m ) *((10 ^2 cm)/(1m) )`

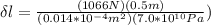
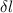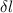`\delta l` = 0.5 cm

Thus, the elongation of the wire when the mass is at its lowest point on the path = 0.5 cm

b)

Using Newton's second law of motion also for the mass at its highest point of the path; we have:

`T +mg = m R \omega ^2`

`T = mR \omega^2- mg`

`T = m( R \omega^2 - g)`

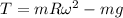
Replacing our given values ; we have:

`T = 12.0( 0.5(12.57)^2 - 9.8)`

`T = 12.0( 0.5(158.0049)-9.8)`

`T = 12.0( 79.00245 - 9.8)`

`T = 12.0( 69.20245)`

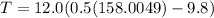
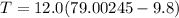
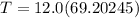
T = 830.4294 N

T = 830 N

Determining the elongation
`\delta l` in the wire by using the equation

Y =
`(Tl)/(AY)`

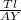
Making
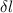`\delta l` the subject of the formula; we have

`\delta l = (Tl)/(AY)`

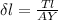
where ;

l = length of the wire

T =Tension in the wire

A = cross - sectional area

Y = young's modulus

Then;

`\delta l = ((830 N)(0.5m))/((0.014*10^(-4)m^2)(7.0*10^(10)Pa))`

`\delta l` =
`( 0.00424 m ) *((10 ^2 cm)/(1m) )`

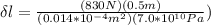
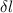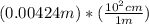
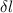`\delta l` = 0.42 cm

Thus, the elongation of the wire when the mass is at its highest point on the path = 0.42 cm