Answer:
Probability that the first machine produces an acceptable cork is 0.7887
Probability that the second machine produces an acceptable cork is 0.9329.
Explanation:
We are given that there are two machines available for cutting corks intended for use in wine bottles. The first produces corks with diameters that are normally distributed with mean 3 cm and standard deviation 0.08 cm. The second machine produces corks with diameters that have a normal distribution with mean 3.04 cm and standard deviation 0.04 cm.
Acceptable corks have diameters between 2.9 cm and 3.1 cm.
Let
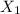 = diameter for producing corks using first machine
= diameter for producing corks using first machine
The z-score probability distribution for normal distribution is given by;
Z =
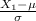 ~ N(0,1)
~ N(0,1)
where,
 = mean diameter of first machine = 3 cm
= mean diameter of first machine = 3 cm
 = standard deviation of first machine = 0.08 cm
= standard deviation of first machine = 0.08 cm
So,
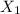 ~ Normal(
~ Normal(
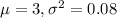 )
)
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
Now, Probability that the first machine produces an acceptable cork is given by = P(2.9 cm <
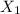 < 3.1 cm) = P(
< 3.1 cm) = P(
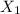 < 3.1 cm) - P(
< 3.1 cm) - P(
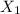
 2.9 cm)
2.9 cm)
P(
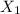 < 3.1 cm) = P(
< 3.1 cm) = P(
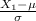 <
<
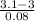 ) = P(Z < 1.25) = 0.89435
) = P(Z < 1.25) = 0.89435
P(
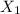
 2.9 cm) = P(
2.9 cm) = P(
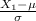

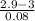 ) = P(Z
) = P(Z
 -1.25) = 1 - P(Z < 1.25)
-1.25) = 1 - P(Z < 1.25)
= 1 - 0.89435 = 0.10565
{Now, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.25 in the z table which has an area of 0.89435.}
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.25 in the z table which has an area of 0.89435.}
Therefore, P(2.9 cm <
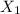 < 3.1 cm) = 0.89435 - 0.10565 = 0.7887
< 3.1 cm) = 0.89435 - 0.10565 = 0.7887
Let
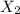 = diameter for producing corks using second machine
= diameter for producing corks using second machine
The z-score probability distribution for normal distribution is given by;
Z =
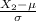 ~ N(0,1)
~ N(0,1)
where,
 = mean diameter of second machine = 3.04 cm
= mean diameter of second machine = 3.04 cm
 = standard deviation of second machine = 0.04 cm
= standard deviation of second machine = 0.04 cm
So,
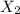 ~ Normal(
~ Normal(
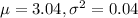 )
)
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
Now, Probability that the second machine produces an acceptable cork is given by = P(2.9 cm <
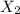 < 3.1 cm) = P(
< 3.1 cm) = P(
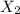 < 3.1 cm) - P(
< 3.1 cm) - P(
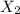
 2.9 cm)
2.9 cm)
P(
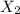 < 3.1 cm) = P(
< 3.1 cm) = P(
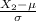 <
<
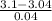 ) = P(Z < 1.50) = 0.93319
) = P(Z < 1.50) = 0.93319
P(
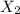
 2.9 cm) = P(
2.9 cm) = P(
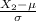

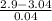 ) = P(Z
) = P(Z
 -3.50) = 1 - P(Z < 3.50)
-3.50) = 1 - P(Z < 3.50)
= 1 - 0.99977 = 0.00023
{Now, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.50 and x = 3.50 in the z table which has an area of and respectively.}
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 1.50 and x = 3.50 in the z table which has an area of and respectively.}
Therefore, P(2.9 cm <
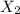 < 3.1 cm) = 0.93319 - 0.00023 = 0.9329
< 3.1 cm) = 0.93319 - 0.00023 = 0.9329
- Now after observing both the probabilities it is clear that second machine is more likely to produce an acceptable cork because it has higher probability as compared to first machine.