Given:
CD = 18 cm
CE = 8 cm
To find:
The length of the radius of the circle A.
Solution:
Let the radius of the circle be x.
AD = AE = x
CA = CE + AE
CA = 8 + x
The angle between a tangent and radius is always right angle.
Therefore triangle ADC is a right triangle.
Using Pythagoras theorem:
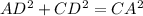
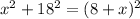
Using algebraic identity:
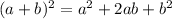
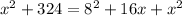
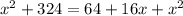
Subtract x² from both sides.
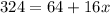
Subtract 64 from both sides.

Divide by 16 on both sides, we get
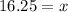
The length of the radius of the circle is 16.25 cm.