Question

Water is drained out of tank, shaped as an inverted right circular cone that has a radius of 6cm and a height of 12cm, at the rate of 3 cm3/min. At what rate is the depth of the water changing at the instant when the water in the tank is 9 cm deep? Give an exact answer showing all work and include units in your answer. (10 points)

Answer 1

Therefore the depth of the water is changing at the instant when the water in the tank is 9 cm deep at rate
`(4)/(27\pi)`
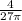
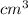`cm^3`/ min.

Explanation:

Given that,

Radius of the cone(r)= 6 cm

Height of the cone (h)= 12 cm

`\therefore \frac rh =\frac 6{12}`

`\Rightarrow h=2r`

`\Rightarrow r=\frac h2`

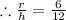
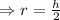
The volume of the cone is (V)
`=\frac13 \pi r^2 h`

`\therefore V=\frac13 \pi r^2 h`

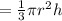
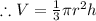
Putting
`r=\frac h2`

`\therefore V=\frac13 \pi (\frac h2)^2 h`

`\Rightarrow V=\frac1 {12} \pi h^3`

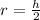
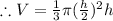
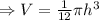
Differentiating with respect to t

`(dV)/(dt)=\frac 1{12}\pi . (3h^2) (dh)/(dt)`

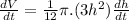
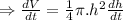`\Rightarrow (dV)/(dt)=( 1)/(4)\pi . h^2(dh)/(dt)` ....(1)

Given that water is drained out of tank at the rate 3
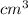`cm^3`/ min.

It means the rate change of volume is 3
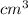`cm^3`/ min that is
`(dV)/(dt)=3 \ cm^3/min`

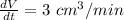
Putting the value of
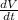`(dV)/(dt)` in equation (1)

`\therefore 3=( 1)/(4)\pi . h^2(dh)/(dt)`

`\Rightarrow (dh)/(dt)=(3* 4)/(\pi h^2)`

`\Rightarrow (dh)/(dt)=(12)/(\pi h^2)`

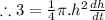
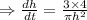
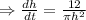
To find the rate of the depth of water changing at 9 cm depth, we need to put h=9 cm in the above equation.

`\therefore (dh)/(dt)|_(h=9)=(12)/(\pi .9^2)`

`=(4)/(27\pi)`
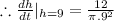
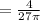
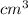`cm^3`/ min.

Therefore the depth of the water is changing at the instant when the water in the tank is 9 cm deep at rate
`(4)/(27\pi)`
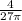
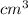`cm^3`/ min.