Answer:
- Ball 1 will move backward at 7.89 m/s
- Ball 2 will move forward at 4.67 m/s
Step-by-step explanation:
In an elastic collision, both the total momentum and the total kinetic energy of the system are conserved.
The conservation of the momentum can be written as:
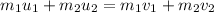
where
 is the mass of ball 1
is the mass of ball 1
 is the mass of ball 2
is the mass of ball 2
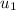 is the initial velocity of ball 1
is the initial velocity of ball 1
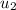 is the initial velocity of ball 2
is the initial velocity of ball 2
 is the final velocity of ball 1
is the final velocity of ball 1
 is the final velocity of ball 2
is the final velocity of ball 2
The conservation of kinetic energy can be written as
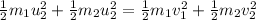
Working together the two equations, it is possible to find two expressions for the final velocities in terms of the initial velocities:
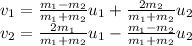
In this problem we have:
 since the mass of the two balls is identical
since the mass of the two balls is identical
 is the initial velocity of ball 1
is the initial velocity of ball 1
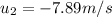 is the initial velocity of ball 2
is the initial velocity of ball 2
Substituting into the equations, we find the final velocities:
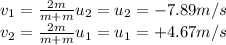
Therefore:
- Ball 1 will move backward at 7.89 m/s
- Ball 2 will move forward at 4.67 m/s