Question

Pierce Manufacturing determines that the daily​ revenue, in​ dollars, from the sale of x lawn chairs is
`R(x) = 0.005 x^3 + 0.01 x^2 + 0.5 x`. ​Currently, Pierce sells 50 lawn chairs daily. ​

a) What is the current daily​ revenue? ​
b) How much would revenue increase if 55 lawn chairs were sold each​ day? ​
c) What is the marginal revenue when 50 lawn chairs are sold​ daily? ​
d) Use the answer from part​ (c) to estimate ​R(51​), ​R(52​), and ​R(53​).

Answer 1

The correct answers are a) $652.5; b) $212.375; c) $13.05; d) R(51) = $689.52, R(52) = $732.68, R(53) = $775.125.

Explanation:

Revenue function of Pierce Manufacturing from the sale of x lawns is given by R(x) = 0.005
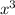`x^(3)` + 0.01
`x^(2)` + 0.05x.

Daily, Pierce Manufacturing is selling 50 lawn chairs.

a) Current daily revenue, i.e. x is 50 = 625 + 25 + 2.5 = $ 652.5.

b) Increase in revenue by selling 5 more chairs = R(55) - R(50) = $ (864.875 - 652.50) = $ 212.375.

c) Marginal Revenue function is given by dividing the revenue function by quantity. Therefore MR(x) = 0.005
`x^(2)` + 0.01x + 0.05.

Value MR(50) = 12.5 + 0.5 + 0.05 = $ 13.05.

d) The value of R(51) = MR(51) × 51 = $ (13.52 × 51) = $ 689.52.

The value of R(52) = MR(52) × 52 = $ (14.09 × 52) = $ 732.68.

The value of R(53) = MR(53) × 53 = $ (14.625 × 53) = $ 775.125.