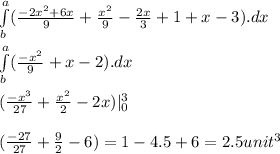Question

Use a double integral to find the volume of the solid in the first octant bounded by the plane determined by the three non-colinear points P(3, 0, 0), Q(0, 1, 0),R(0, 0, 2). Draw a picture of the volume you are finding.

Answer 1

2.5 units^3

Explanation:

Given:-

- The solid is bounded by a plane defined by the following points:

P(3, 0, 0), Q(0, 1, 0),R(0, 0, 2)

Find:-

Use a double integral to find the volume of the solid in the first octant bounded by the plane

Solution:-

- Determine the equation of the plane. Compute two direction vectors d1 and d2 that lie on the plane:

d1 = P - Q

d1 = (3, 0, 0) - (0, 1, 0) = (3,-1,0)

d2 = P - R

d2 = (3, 0, 0) - (0, 0, 2) = (3,0,-2)

- Find the a vector "normal" - n to the plane by cross product formulation of direction vectors (d1 and d2) that lie on the plane:

`n = d1xd2 = \left[\begin{array}{c}3&-1&0\end{array}\right] x \left[\begin{array}{c}3&0&-2\end{array}\right] = \left[\begin{array}{ccc}3&-1&0\\3&0&2\end{array}\right] = \left[\begin{array}{c}-2&-6&3\end{array}\right]`

- The equation of plane is:

n.(x,y,z) = n.P

-2x -6y + 3z = -6

- The function of one variable would be:

z = (2/3)x + 2y - 2

- The double integration formulation would be:

`\int\limits^a_b \int\limits^c_d f(z) dy.dx\\\\\int\limits^a_b \int\limits^c_d ((2x)/(3) + 2y - 3) dy.dx\\\\\int\limits^a_b ((2xy)/(3) + y^2 - 3y) |_c^d.dx`

- Where the limits (c and d) are defined by planar (x-y) projection of plane (n) :

y = d = -(1/3)x + 1

c = 0

- Evaluate the limits:

`\int\limits^a_b ((-2x^2 + 6x)/(9) + (x^2)/(9) -(2x)/(3) +1 + x - 3) .dx\\\\\int\limits^a_b ((-x^2 )/(9) + x - 2) .dx\\\\((-x^3 )/(27) + (x^2)/(2) - 2x)|^3_0\\\\((-27 )/(27) + (9)/(2) - 6) = 1 - 4.5 + 6 = 2.5 unit^3`