Question

Consider a binomial experiment with n = 10 and p = 0.10. (a) Compute f(0). If required, round your answer to four decimal places. .3487 (b) Compute f(2). If required, round your answer to four decimal places. .0043 (c) Compute P(x ≤ 2). If required, round your answer to four decimal places. 1.1666 (d) Compute P(x ≥ 1). If required, round your answer to four decimal places. (e) Compute E(x). (f) Compute Var(x) and σ. If required, round Var(x) answer to one decimal place and σ answer to four decimal places. Var(x) = σ =

Answer 1

(a) The value of f (0) is 0.3487.

(b) The value of f (2) is 0.1937.

(c) The value of P (X ≤ 2) is 0.9298.

(d) The value of P (X ≥ 1) is 0.6513.

(e) The value of E (X) is 1.

(f) The value of V (X) is 0.9 and σ is 0.9487.

Explanation:

The random variable X follows a Binomial distribution with parameter n = 10 and p = 0.10.

The probability mass function of X is:

`P(X=x)={10\choose x}0.10^(x)(1-0.10)^(10-x);\ x=0,1,2,3...`

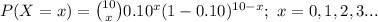
(a)

Compute the value of f (0) as follows:

f (0) = P (X = 0)

`={10\choose 0}0.10^(0)(1-0.10)^(10-0)\\=1* 1* 0.348678\\=0.348678\\\approx0.3487`

Thus, the value of f (0) is 0.3487.

(b)

Compute the value of f (2) as follows:

f (2) = P (X = 2)

`={10\choose 2}0.10^(2)(1-0.10)^(10-2)\\=45* 0.01* 0.43047\\=0.1937115\\\approx0.1937`

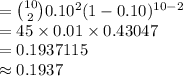
Thus, the value of f (2) is 0.1937.

(c)

Compute the value of P (X ≤ 2) as follows:

P (X ≤ 2) = P (X = 0) + P (X = 1) + P (X = 2)

`=\sum\limits^(0)_(2) {{10\choose x}0.10^(x)(1-0.10)^(10-x)}\\=0.3487+0.3874+0.1937\\=0.9298`

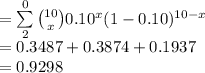
Thus, the value of P (X ≤ 2) is 0.9298.

(d)

Compute the value of P (X ≥ 1) as follows:

P (X ≥ 1) = 1 - P (X < 1)

= 1 - P (X = 0)

= 1 - 0.3487

= 0.6513

Thus, the value of P (X ≥ 1) is 0.6513.

(e)

Compute the expected value of X as follows:

`E(X)=n* p`

`=10* 0.10\\=1`

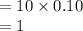
Thus, the value of E (X) is 1.

(f)

Compute the variance of X as follows:

`V(X)=np(1-p)`

`=10* 0.10* (1-0.10)\\=0.90`

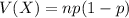
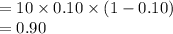
Compute the standard deviation of X as follows:

`SD(X)=√(V(X))`

`=√(0.90)\\=0.94868\\\approx0.9487`

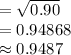
Thus, the value of V (X) is 0.9 and σ is 0.9487.