Answer:
THe second lines connects at the x value, x = 6.
Explanation:
We will asume that the pdf is 0 for x<0 and that once the function reaches the x axis, it will be 0 from that point on. Recall that given a function f(x),in order for it to be a probability density function, it must happen that
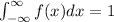
Attached you will see an image that ilustrates the function f(x). IN this case, the integral represents the area under the curve. Note that we are given that the points (0,0.25) and (2,0.25) are joined by a line, and the we have another line that connects the points (2,0.25) and the (h,0). We are asked to calculate h.
Note that the area under the curve is divided in the regions 1 and 2. The region 1 is a rectangle of height 0.25 and base 2, hence it's area is 0.5. Since the total area under the curve must add to 1, we must have that the region 2 has an area of 0.5
Note that the region 2 is a triangle of height 0.25 and base h-2. So, recalling the area of a triangle, we have that
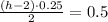
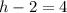 which implies that h=6 which is our final answer.
which implies that h=6 which is our final answer.