Question

In a recent poll of 1,200 homeowners in the United States, one in five homeowners reports having a home equity loan that he or she is currently paying off. Using a confidence coefficient of 0.99, derive the interval estimate for the proportion of all homeowners in the United States that hold a home equity loan.

Answer 1

Interval estimate for the proportion of all homeowners in the United States that hold a home equity loan lie between (.17033 , .22967 ) or 17% to 22.9%

Explanation:

Given -

In a recent poll of 1,200 homeowners in the United States, one in five homeowners reports having a home equity loan that he or she is currently paying off.

If one in five homeowners reports having a home equity loan then for 1200 homeowners =
`(1200)/(5)` = 240 homeowners reports having a home equity loan.

Sample proportion
`(\widehat{p})` =
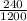`(240)/( 1200)` = 0.2

confidence coefficient = 0.99

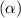`(\alpha)` = 1 - confidence coefficient = 1 - 0.99 = .01

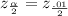`z_{(\alpha)/(2)} = z_{(.01)/(2)}` = 2.58

interval estimate for the proportion of all homeowners in the United States that hold a home equity loan

=
`\widehat{p}\pm z_{(\alpha)/(2)}\sqrt\frac{{\widehat{p}( 1 - \widehat{p})}}{n}`

=
`0.2\pm z_{(.01)/(2)}\sqrt\frac{{0.2( 1 - 0.2)}}{1200}`

=
`0.2\pm 2.58* \sqrt\frac{{0.2( 0.8)}}{1200}`

=
`0.2\pm .02967`

=
`(0.2 - .02967 ) , (0.2 + .02967)`

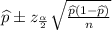
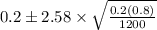
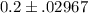
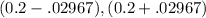
= (.17033 , .22967 )